What in the wordle?

Jo recently found and shared with me this online word game called Wordle (which actually has a really cool backstory). The rules are simple, and the website explains them well:

To make it more clear, here’s an example where I was able to guess the wordle in 4 tries:

From the first guess, I learned that the word ends in “D” and has an “A” somewhere not in the 2nd position (and has no “F”, “C” or “E”). The second guess told me that the “A” was also not in the 3rd position (and also had no “G”, “L” or “N”). The third guess yielded the “R”, and from there I could only think of one word that fit the constraints (TRIAD), allowing me to solve it in four tries.

Jo and I have been solving the daily puzzles separately, and we’ve usually been able to figure out the answer in 4 tries, which seemed surprisingly low to us! Jo asked me whether I thought that was a good score or not, and it struck me that there was a way to explore that question with information theory.

Background

Information theory defines the “entropy” or “information” of a random variable as the number of bits required to describe it. How does this apply to a guessing game? Let’s look at a simpler example.

Twenty Questions is a game with a simple premise — can you guess a word that I’m thinking of by asking 20 yes/no questions? To those who haven’t played, it may be surprising to learn this is quite easy to do — Cheap toys are already able to guess your word with 20 questions.

How? Well, each question can halve the number of remaining options, if well chosen. If you were able to choose the perfect question each time, you could go from 8 choices to 4, to 2, to 1 with 3 questions, or from 1000 choices to 1 with 10 questions, or from 1,000,000 choices to 1 with 20 questions.

Since finding an item out of 1,000,000 choices can be done with 20 well-chosen questions, we can say that the random variable that selects one of them has roughly 20 bits of information. In general, it takes log2(N) bits to describe a choice among N items.

One important thing to note is that questions are good only if they roughly divide the search space in half. A question like “are you thinking of a crocodile?” is a poor choice since if you’re wrong, you only eliminate one possible choice, leaving N-1 remaining. Another nuance is that in the information-theoretic setting you would not be able to choose your questions based on the answers to previous ones, but I’ll ignore that point for this post.

Applying it to Wordle

So how does information theory apply to Wordle? The first question we can try to answer is: “ How many bits of information are required to guess a five-letter word?”. This is actually straightforward — Once we know how many five-letter words there are, by definition, the information content of choosing one of them is just log2(N) bits.

So all we need to do is agree on what a reasonable five-letter english word is. I first tried using two sources of data:

1. words_alpha (contains 477k english words)
2. top 10,000 most commonly searched english words according to Google

For each dataset, I filtered down to 5-letter words, leaving me with ~16,000, and ~1,600 words, respectively. I took a peek at the first dataset and didn’t like that there were words like “aalii” and “goety”. The second one contained all “normal” words but didn’t have some simple words like “troll”, so I wasn’t happy with that either.

I eventually found the source code and the actual word list that Wordle uses here — it contains ~270k works and ~12.5k 5-letter words. This was the best choice to use, since the answer will match the same data source as the game itself. This equates to ~14 bits of information.

Wordle guesses

The next question to answer is how much information we gain from a Wordle guess. Calculating the information gain for a Twenty Questions guess was easy, since each question has exactly two outcomes (one bit). But you learn some more complex information from a Wordle guess: which letters are not in the word, and which are in the word at the right and wrong locations. How do we calculate the information gain for that?

A bit of inspiration

I left this question in the back of my mind for a few days, since I didn’t see an obvious approach. Then one day last week, I was driving home when I ran out of podcasts (I normally have them queued up and downloaded) so I turned my attention back to it.

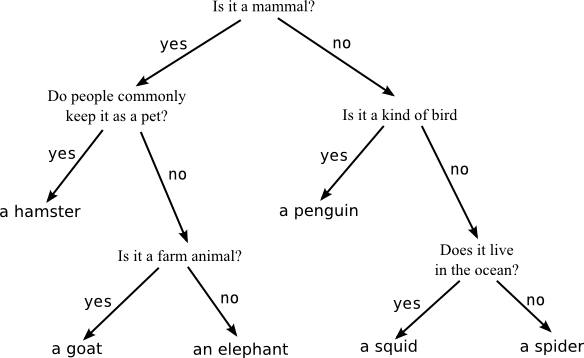
After trying a few different angles, I realized there was a simple way to think about it. Every time we guess a word the game will return a “coloring” of it depending on the answer. We can think of each “word-guess” as consisting of 5 “letter-guesses”. Each “letter-guess” will be colored one of 3 ways (green, yellow, or gray).

Using some simple combinatorics, this mean each “word-guess” can potentially have 3⁵or 243 different colorings. Since the game will tell us which of the possible colorings is the true coloring, this means that a guess actually gives us log2(243) or almost 8 bits of information.

Information can be added and subtracted directly — If each guess removes 8 bits of information from a 14-bit variable, then the first guess should leave us with only 6 bits of information, the second guess should narrow it down to a single choice, then the third guess should be correct. It’s then no surprise that Jo and I can guess the word within 3 or 4 tries. So mystery solved!

Except not quite. That definition of information actually gives us an upper bound on the amount on how useful a guess can be. The actual information gain depends on the word we choose and its relation with the other words. Intuitively, some words should be very helpful (like a question that splits the space in half in 20 questions), while some are close to useless.

Going deeper

Even though I had answered my original question, I wasn’t totally satisfied. I had a new question in my mind: What is the “best” word we can guess, and how much information are we able to get with it? To answer these we need to understand exactly what makes a guess “good”.

To get some intuition on why different words are better or worse guesses, let’s look at a smaller example. Imagine we are playing Wordle, but only trying to choose between 7 different two-letter words:

[“oh”, “ow”, “hi”, “to”, “ab”, “ho”, “ah”]

If we guess a word, we will get back some coloring of it. Let’s draw a table consisting of all the different possible colorings we might receive for a guess (3 colors, 2 letters, so 9 colorings) and see which answers correspond to those colorings.

If we guess “oh”, we get a chart that looks like this:

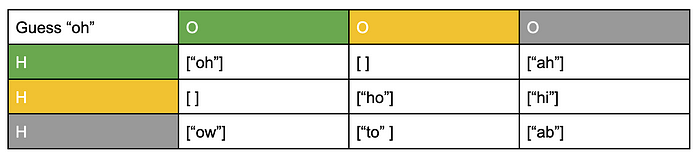
This is great choice for a guess, because we will know for sure what the correct answer is after we get a coloring back. Each coloring corresponds only to a single answer, which means we can just look up the answer in the above table once we get the coloring.

On the other hand, if we guess “ab”, we get a chart like this:

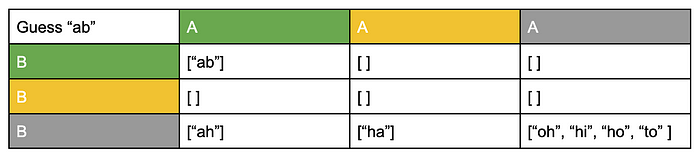
This is not as good of a guess, since there’s a 4/7 chance that we’ll receive a “gray-gray” coloring, and we’ll still have no idea which of the remaining 4 words is the real answer.

“Shut up and calculate”

It turns out that we can generalize the intuition above — a discrete random variable has maximum entropy when the outcomes are equally likely. This is exactly the same principle that rewarded us for choosing questions in Twenty Questions that evenly divide the space. For our purposes, the “best” guess is the one that most evenly divides the outcome space. If there are N words and M different colorings, we want the word that most closely puts N/M words in each coloring. In our case, with 12,500 words and 243 outcomes, we should aim for around 50 words per coloring.

The definition of entropy, below, formalizes what it means to be further from or closer to an even distribution:

The important thing to know about this equation is that we can compute it. P(xi) correspond to the number of entries in each cell of the tables above (divided by N), so in the two-letter example, “oh” would have a probability vector that looks like [1/7,0,1/7,0,1/7,1/7,1/7,1/7,1/7] and “ab” would have a probability vector that looks like [1/7,0,0,0,0,0, 1/7/,1/7, 4/7]. Those correspond to entropies of ~2.8 and ~1.7, respectively. This matches our intuition that “oh” was a better guess than “ab”.

So in order to choose the best 5-letter word, we just need to compute a similar table (but with 243 cells) for each word and calculate the entropy from it. I wrote a program to compute entropy values for each word, and print out the highest one, which happens to be “t̶a̶r̶e̶s̶”(edit: soare is actually the correct word, see bottom of post for update). “Tares” came in with an entropy of ~6.2 (compared to theoretical “max” entropy of ~8). (The worst is xylyl with an entropy of 2.0, it apparently refers to a group of chemical compounds).

I also added the ability to recompute the best word after each guess (each guess further constrains the set of possible words, but the same principle as above can be reused at each step), giving me a pretty effective way to solve Wordles with maximum efficiency. I tried it out on today’s Wordle and it did pretty well — you can try the code yourself here:

Conclusion

So we answered the original question and also a couple more that came up through thinking about the problem. I’m pretty satisfied with this, but one question I’m still wondering about is whether I really need to compute the entropy for every word in order to get the best score, or if there’s a more efficient way to do it. This way works okay, but it took my computer a while to chug through the computations. I had to rewrite my code from python to C++ to get it to finish in a reasonable amount of time. If I increased the vocabulary size or allowed non-vocabulary words to be guessed, this approach wouldn’t scale well. If anyone has ideas on how to speed this up or take a less computational approach, I’d love to hear it!

Update 1 (01/08/21):

Looking around on the internet, I realized others like Tyler Glaiel have come up with different best first words than me. I’ve also gotten a lot of responses from friends telling me they only try “tares” now, which made me realize I had a responsibility to double-check my work, lest people underachieve on their wordles.

One discrepancy to look into was that Tyler had mentioned there were two separate word lists for Wordle; one for words that can be the Wordle (valid solutions) and one for words you can guess (valid guesses). The valid solution list contains~2.5k words, while the valid guess list contains~12.5k words.

My earlier analysis wasn’t distinguishing between those two lists. If you remember, a word that has good entropy is one that divides the solution space evenly. If the distribution of letter-positions in solution space is very different than the guess space, that would result in a different “best guess” than I initially suggested.

I wasn’t able to find the solution list, but Tyler shared the list he found from the source code. Re-running my program, accounting for the smaller list of solution words gave me “soare” as the best word, with an entropy of ~5.89 (tares is down to 5.74 now). My hypothesis is that “tares” drops off a bit because the solution list is curated to avoid words that end in “s”.

Interestingly, though, in his post, Tyler first crowned “soare” using a different scoring system than me but ended up using “roate” after switching to a more similar scoring system. “roate” is the second-highest entropy word by my calculation, so I’m not sure what we did differently.

I also wanted to know whether there were other words that are almost as good, and more generally what the distribution of entropies look like, so I plotted a histogram of the entropies below:

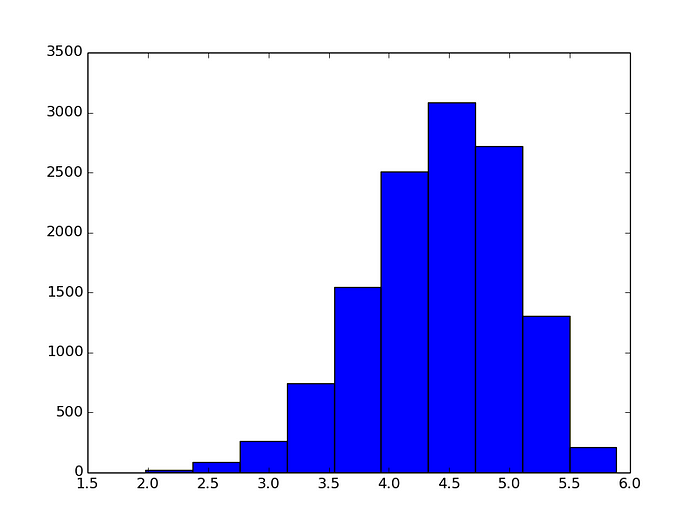
Overall it looks like there are plenty of first guesses which are “good enough” to do well with. Even if you want to limit yourself to the cream of the crop (entropy > 5.8), you have several diverse options that I’ve listed below:

soare 5.88596
roate 5.88278
raise 5.87791
raile 5.86571
reast 5.86546
slate 5.85578
crate 5.83487
salet 5.83458
irate 5.8314
trace 5.83055
arise 5.82094
orate 5.81716
stare 5.80728

Personally, I’ll be using “raise” for now since I don’t think either of the words above it are words I’ve ever used, but to each their own!

Update 2(01/17/21):

Some friends had a couple of interesting follow-up questions that I followed up on.

One such question: “What is the worst-case number of guesses to find the answer, following the maximum-entropy strategy?”. I computed this using brute force and found out all Wordle words would be guaranteed to be found in 6 guesses , which is, interestingly, exactly the number that we are allotted.

I should also mention that entropy is a great way to choose the “expected” best word, but not the best way to choose the “worst-case” best word. Some hilariously evil version of the game like Absurdle has a different optimal solver — rather than computing the max-entropy word, we would choose the min-max solution: Pick the word that has the smallest max-size partition.

Another question: “How much harder does playing in hard mode actually make the game?”. Hard mode is a game setting where guesses are restricted to include any “green” letters from previous guesses. Since it’s a restriction on the words that can be guessed, it can only make the game harder. But how much harder?

To answer this, I analyzed each of the 243 partitions that we might end up in after guessing “soare”. For each partition, I calculated what the optimal word was in “hard mode” and “easy mode”, and how much entropy each word gave us. The “easy mode” word always gave at least as much entropy, but a lot of the time the same word or one with equal entropy was chosen, meaning there was no “advantage” to using the full set of guess words.

Then, in order to understand what the “expected advantage” was, I simply applied the formula for “expected value”, where the probability of a partition is proportional to its size.

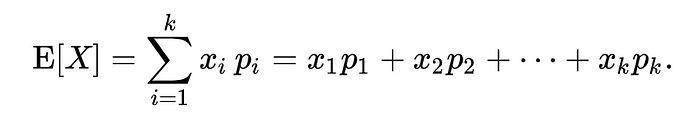
This yielded an expected entropy advantage of 0.29 bits for playing in “not-hard mode” (for just the second guess). This seems to be pretty small, and matches the intuition that I and a lot of my friends had that “hard mode” doesn’t seem that much harder than normal mode. The small advantage does exist for the majority of words though — of the 2315 possible solutions, 1724 of them have an easier guess available in not-hard mode.

Thank you to Chris Tai-yi Lee and Misha Chernov for the suggested follow-up questions!